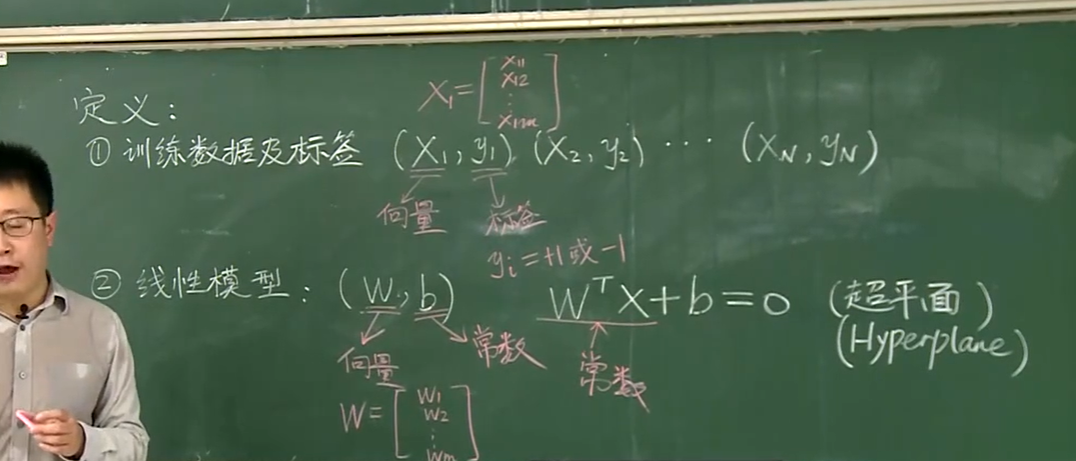深度学习入门2

学习资源：

1. （全面）Machine Learning：，Tom M. Mitchell 机械工业出版社 2003年
2. 统计学习方法，李航，清华大学出版社，2012
3. Machine Learning：A Probabilistic Perspective，K.P Murphy
4. 视频课程：Stanford web course by Andrew Ng
5. 视频课程：Stanford web course by Fei-fei Li

没有免费午餐定理（No Free Lunch Theorem）

如果我们不对特征空间有先验假设，则所有算法的平均表现是一样的

支持向量机（Support Vector Machine）

在样本数比较少的情况下，可以得到比较好的结果（小样本方法）

支持向量机

1.线性模型

线性可分：训练集和样本集可以用一条直线分开

2.非线性模型

线性不可分：训练集和样本集不可以用一条直线分开

理论关键点1：如何定义一条线，将训练集和样本集恰当的分开（恰当=在误差上，不偏袒训练或者样本集任一方）

答：

定义一个衡量指标——向训练集和样本集的方向，分别平移此线，在刚好碰到训练集和样本集的某些点时，能够使平移后的两条线距离最大

符合衡量指标的线条有很多（平行线），如何确定一条恰当的线——取所有平行线中，最中间的那条（到训练集和样本集距离相等的那条）

间隔d定义：关键点1中的分割线，向到训练集和样本集平移，刚好分别与训练集和样本集的某些点相碰，产生的两条平行线间的距离

支持向量定义：分割线的所有平行线之中，刚好分别与训练集和样本集的某些点相碰的两条平行线碰到的点，所代表的向量（support vectors）

ps：正是因为分割线的定义只是基于支持向量（支持向量仅占训练集和样本集的少部分），所以支持向量机依靠少量数据就能实现