深度学习入门1

内容概述

神经网路与多层感知机：基础知识、激活函数、反向传播、损失函数、权值初始化和正则化
卷积神经网络、循环神经网络
人工智能>机器学习>人工神经网络（以神经元形式连接的机器学习模型）>深度学习

学习资源：

1. 吴恩达 www.deeplearning.ai
2. 李宏毅 B站搜索
3. 花书《deep learning》https://github.com/exacity/deeplearningbook-chinese
4. 西瓜书《机器学习》周志华

人工神经网络

概念：

perception（感知机）

activation function（激活函数）

back propagation（反向传播）

激活函数

激活函数引用目的：

1. 令多层感知机真正的成为多层，而不是退化为一层
2. 引入非线性，使网络可以逼近任意非线性函数（万能逼近定理，universal approximator）

激活函数需要具备的性质：

1. 连续并可导（允许少数点不可导），便于利用数值优化的方法学习网络参数（什么叫数值优化？）
2. 激活函数和其导函数要尽量简单，有利于提高网络计算效率
3. 激活函数的导函数的值域要在合适区间，否则会影响训练效率和稳定性

常见激活函数：

Sigmoid函数、tanh函数、Relu函数

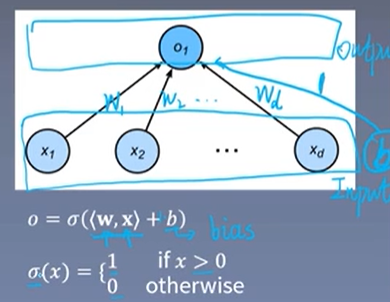
单层感知机

输入*权重=输出（无隐藏层）

F（<Xn·Wn>+偏置b）=O——以向量乘法<A·B>（单行矩阵乘法）来表示单层感知机计算，再放进F函数（激活函数）

上图为单层感知机，其缺点：无法解决异或问题

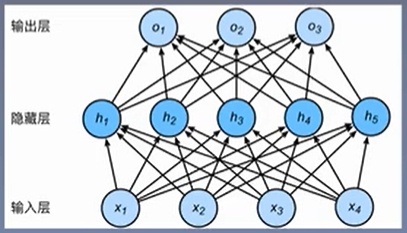
多层感知机（Multi Perception，MLP）

在单层感知机的基础上，添加一个或多个隐藏层

输入 * 权重 = 输出（隐藏层1）—>隐藏层1 * 权重 = 输出（隐藏层2）…隐藏层n * 权重=输出层

矩阵表示：X1*n表示输入矩阵；W1n*m表示权重矩阵(n-输入，m-输出)；H1*m表示隐藏层矩阵；W2m*k；O1*k表示输出矩阵

​ X*W1+b1=H

​ H*W2+b2=O(b是偏置项)

ps：这部分其实不对，输入*权重的结果经过activation function 才会成为H

多层感知机的激活函数：如果无激活函数，多层感知机会退化为单层网络，
$$
\begin{aligned}
\mathbf{H} &=\mathbf{W}{1} \mathbf{X}+\mathbf{b}{1}\
\mathbf{O} &=\mathbf{W}{2} \mathbf{H}+b{2} =\mathbf{W}{2}(\mathbf{W}{1} \mathbf{X}+\mathbf{b}{1})+\mathbf{b}{2} =\mathbf{W}{2}\mathbf{W}{1}\mathbf{X}
+\mathbf{W}{2}\mathbf{b}{1}+\mathbf{b}_{2}
\end{aligned}
$$
X经过两层权重计算输出结果O，通过计算，结果可以等效成X经过W1W2的乘积（即一层权重网络），然后加上后半部分，也就是说，X经过两层网络，但实际结果可以等效成经过一层网络，这就叫退化成单层网络

所以在经过第一层权重计算后，要通过激活函数（为什么W2要转置呢？）
$$
\begin{aligned}
\mathbf{H} &=\mathbf{F}\left(\mathbf{W}{1} \mathbf{X}+\mathbf{b}{1}\right) \
\mathbf{O} &=\mathbf{W}{2}^{T} \mathbf{H}+b{2}
\end{aligned}
$$

反向传播（Back propagation）

机器学习可以看做是数理统计的一个应用。在数理统计中一个常见的任务就是拟合，也就是给定一些样本点，用合适的曲线（函数）揭示这些样本点随着自变量的变化关系。

深度学习同样也是为了这个目的，只不过此时，样本点不再限定为(x, y)点对，而可以是由向量、矩阵等等组成的广义点对(X,Y)。而此时，(X,Y)之间的关系也变得十分复杂，不太可能用一个简单函数表示。然而，人们发现可以用多层神经网络来表示这样的关系，而多层神经网络的本质就是一个多层复合的函数。借用网上找到的一幅图，来直观描绘一下这种复合关系。

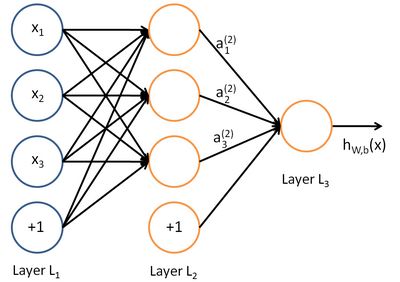
表达式如下（输入x经过加权相乘，然后加偏置向，然后通过激活函数）：

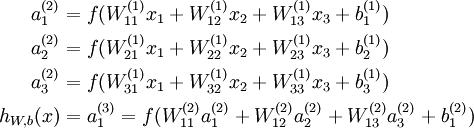
式中的Wij就是相邻两层神经元之间的权值，它们就是深度学习需要学习的参数，也就相当于直线拟合y=k*x+b中的待求参数k和b。

和直线拟合一样，深度学习的训练也有一个目标函数，这个目标函数定义了什么样的权值参数才算一组“好参数”，在机器学习中，一般是采用损失函数（cost function）作为目标，然后，训练目标就是通过调整每一个权值Wij来使得cost达到最小。cost函数也可以看成是由所有待求权值Wij为自变量的复合函数，而且基本上是非凸的，即含有许多局部最小值。但实际中发现，采用我们常用的梯度下降法？就可以有效的求解最小化cost函数的问题。

梯度下降法需要给定一个初始点，并求出该点的梯度向量，然后以负梯度方向为搜索方向，以一定的步长进行搜索，从而确定下一个迭代点，再计算该新的梯度方向，如此重复直到cost收敛。那么如何计算梯度呢？

假设我们把cost函数表示为, 那么它的梯度向量就等于, 其中表示正交单位向量。为此，我们需求出cost函数H对每一个权值Wij的偏导数。而BP算法正是用来求解这种多层复合函数的所有变量的偏导数的利器。

求cost最小值——>使用梯度下降法——>求初始点梯度——>求cost函数对权值W的偏导数——>使用BP算法

概念：从损失函数开始，从后向前传输梯度到第一层

作用：更新权重，使网络输出更接近标签（label）

反向传播的基本原理：微积分的链式求导法则
$$
\begin{equation}
y=f(u), u=g(x) \quad \frac{\partial y}{\partial x}=\frac{\partial y}{\partial u} \frac{\partial u}{\partial x}
\end{equation}
$$
举例子：

作者：Anonymous
链接：https://www.zhihu.com/question/27239198/answer/89853077
来源：知乎

我们以求e=(a+b)*(b+1)的偏导为例。
它的复合关系画出图可以表示如下：

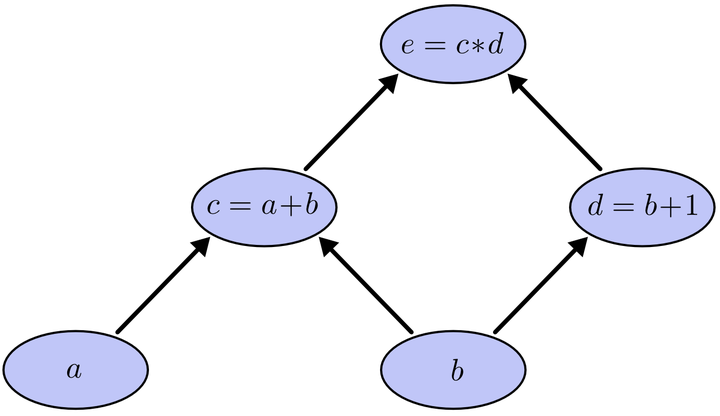
在图中，引入了中间变量c,d。

为了求出a=2, b=1时，e的梯度，我们可以先利用偏导数的定义求出不同层之间相邻节点的偏导关系，如下图所示。

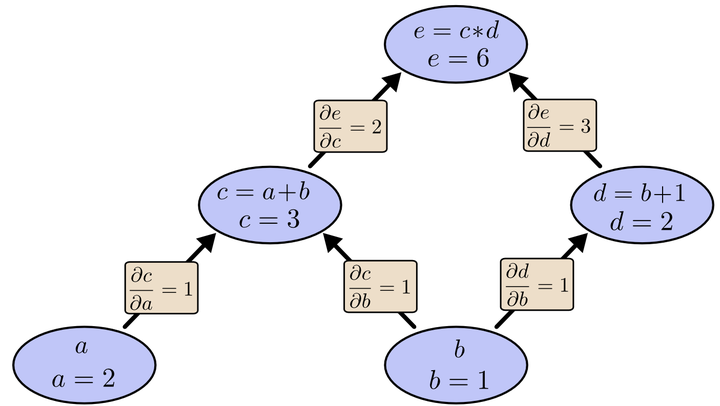
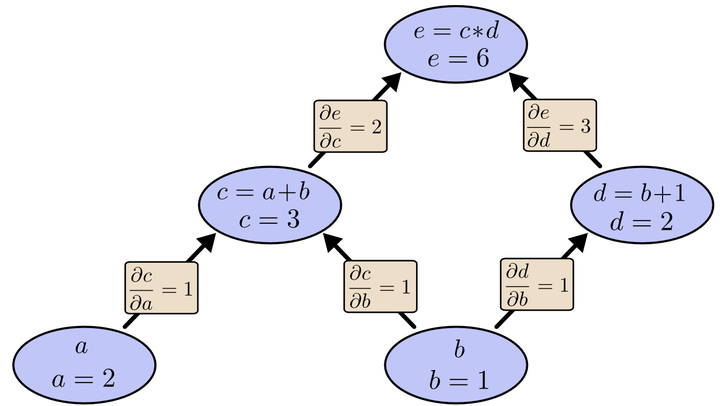
利用链式法则我们知道：
以及。

链式法则在上图中的意义是什么呢？其实不难发现，的值等于从a到e的路径上的偏导值的乘积，而的值等于从b到e的路径1(b-c-e)上的偏导值的乘积加上路径2(b-d-e)上的偏导值的乘积。也就是说，对于上层节点p和下层节点q，要求得，需要找到从q节点到p节点的所有路径，并且对每条路径，求得该路径上的所有偏导数之乘积，然后将所有路径的 “乘积” 累加起来才能得到的值。

这样做是十分冗余的，因为很多路径被重复访问了。比如上图中，a-c-e和b-c-e就都走了路径c-e。对于权值动则数万的深度模型中的神经网络，这样的冗余所导致的计算量是相当大的。

同样是利用链式法则，BP算法则机智地避开了这种冗余，它对于每一个路径只访问一次就能求顶点对所有下层节点的偏导值。
正如反向传播(BP)算法的名字说的那样，BP算法是反向(自上往下)来寻找路径的。

从最上层的节点e开始，初始值为1，以层为单位进行处理。对于e的下一层的所有子节点，将1乘以e到某个节点路径上的偏导值，并将结果“堆放”在该子节点中。等e所在的层按照这样传播完毕后，第二层的每一个节点都“堆放”些值，然后我们针对每个节点，把它里面所有“堆放”的值求和，就得到了顶点e对该节点的偏导。然后将这些第二层的节点各自作为起始顶点，初始值设为顶点e对它们的偏导值，以”层”为单位重复上述传播过程，即可求出顶点e对每一层节点的偏导数。

以上图为例，节点c接受e发送的12并堆放起来，节点d接受e发送的13并堆放起来，至此第二层完毕，求出各节点总堆放量并继续向下一层发送。节点c向a发送21并对堆放起来，节点c向b发送21并堆放起来，节点d向b发送31并堆放起来，至此第三层完毕，节点a堆放起来的量为2，节点b堆放起来的量为21+3*1=5, 即顶点e对b的偏导数为5.

举个不太恰当的例子，如果把上图中的箭头表示欠钱的关系，即c→e表示e欠c的钱。以a, b为例，直接计算e对它们俩的偏导相当于a, b各自去讨薪。a向c讨薪，c说e欠我钱，你向他要。于是a又跨过c去找e。b先向c讨薪，同样又转向e，b又向d讨薪，再次转向e。可以看到，追款之路，充满艰辛，而且还有重复，即a, b 都从c转向e。

而BP算法就是主动还款。e把所欠之钱还给c，d。c，d收到钱，乐呵地把钱转发给了a，b，皆大欢喜。

学习率

作用：控制更新步长（通常小于1）

xi+1=xi-k*f’(xi)

损失函数（Loss function）

损失函数：衡量模型与真实标签之间的差异（针对单样本）
$$
\begin{aligned}
\mathbf{Loss} &=\mathbf{f}\left(\mathbf{y}{o},\mathbf{y}\right) \
\end{aligned}
$$
代价函数（cost function）：针对样本总体
$$
\begin{aligned}
\operatorname{Cost} =\frac{1}{N} \sum{i}^{N} f\left(y_{o}, y_{i}\right)
\end{aligned}
$$
目标函数（objective function）Obj=Cost（要小）+Rgularization Term(正则项，让模型不会过于复杂)

常见损失函数

1. MSE（mean square error）均方误差

$$
M S E=\frac{\sum_{i=1}^{n}\left(y_{o}-y_{lable}\right)^{2}}{n}
$$

2. CE（cross entropy ）交叉熵

$$
H(p, q)=-\sum_{i=1}^{n} p\left(x_{i}\right) \log q\left(x_{i}\right)
$$

为什么用交叉熵来衡量两种分布之间的差异（p表示目标分布，q表示计算出来的分布——要让q逼近p）
$$
\begin{aligned}
&D_{K L}(P | Q)=E_{x-p}\left[\log \frac{P(x)}{Q(x)}\right]=E_{x \sim p}[\log P(x)-\log Q(x)] \
&=\sum_{i=1}^{N} \mathrm{P}\left(\mathrm{x}{i}\right)\left(\log P\left(\mathrm{x}{i}\right)-\log \mathrm{Q}\left(\mathrm{x}{i}\right)\right) \
&H(p, q)=-\sum{i=1}^{n} p\left(x_{i}\right) \log q\left(x_{i}\right) \
&H(\mathrm{x})=E_{x-p}[I(x)]=-E[\log P(x)]=-\sum_{i=1}^{N} p_{i} \log \left(p_{i}\right)
\end{aligned}
$$
相对熵DKL+信息熵H(x) = 交叉熵H(p,q)

优化交叉熵等价于优化相对熵（因为H(P)作为要逼近的目标，信息是确定的）

模型输出的结果可能大于1，不符合概率分布的形式，即无法用交叉熵的形式计算

所以Softmax函数可以实现将数据变换到符合概率分布的形式
$$
y_{i}=S(\boldsymbol{z}){i}=\frac{e^{z{i}}}{\sum_{j=1}^{C} e_{j}^{z_{j}}}, i=1, \ldots, C
$$

权值初始化

随机初始化：从高斯分布中随机采样，对权重赋值，随机初始化（3σ准则：数值分布在均值μ左右3σ的概率要达到99.73%）——初始权重不能太大，不然后面计算结果经过激活函数后，会达到饱和区，梯度就近乎没有了

随机分布的标准差会影响权重大小，如何设置标准差

自适应标准差：Xavier初始化、Kaiming初始化（MSRA法）

正则化方法（Regularization）

正则化是为了减小方差，即减轻过拟合（方差过大导致训练集表现好，测试集表现不好）的方法

误差=偏差+方差+噪声

偏差：度量了学习算法的期望预测与真实结果的偏离程度，即刻画了学习算法本身的拟合能力

方差：度量了同样大小的训练集的变动所导致的学习性能的变化，即刻画了数据扰动所造成的影响

噪声：则表达了在当前任务上任何学习算法所能达到的期望泛化误差的下界

方法1.在目标函数后添加regularization term：

regularization term分L1、L2两种

L1:|Wi|求和

L2:|Wi^2^|求和，也成为权值衰减（weight decay）

方法2.随机失活（dropout）

作用：避免模型过度依赖某个神经元，减轻过拟合

随机的令神经元失活（即将神经元前的权值设为0）

ps：训练和测试时数据尺度会变化（测试时不会执行权重失活操作），所以测试时，神经元输出值要乘P才好对比测试和训练两数据结果？（p为随机失活的概率）

其他正则化方法：batch normalization、layer normalization、instance normalization group normlizaiton