1. Third-Order Factor graph

1.1 图的介绍

Factor graph包含两种node：

1. variable node

   1. 表示individual action: V_y=i, {1,…,n}，假设共有n个individual
   2. 表示a pair of individuals存在interaction的可能性: V_z=(i, j), {n+1,…,n+Cn2}，n个individual理所应当有Cn2个组合

2. factor node

   1. F_y={ (i, j, g(i, j) ) | ∀i, j ∈ V_y, i < j}, {n+Cn2+1,…,n+2×Cn2} ;

      作用：implicitly model 两个V_y的base features和V_z的base feature的关系

   2. F_z={ ( g(i, j), g(i, k), g(j, k) ) | ∀i, j ,k ∈ V_y, i < j < k}, {n+2×Cn2+1,…., n+2×Cn2+Cn3} ;

      作用：implicitly model triplet of people(i,j,k)

关于连接两种node的edge

1. edge连接factor node和variable node（必须一端是factor node，另一端是variable node）

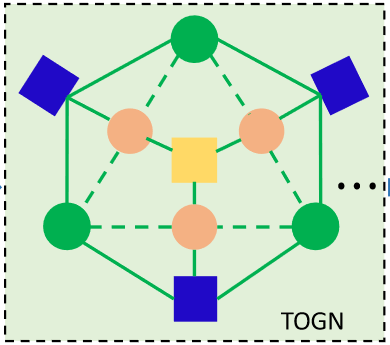
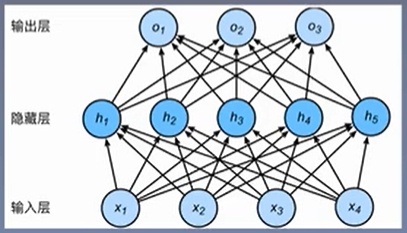
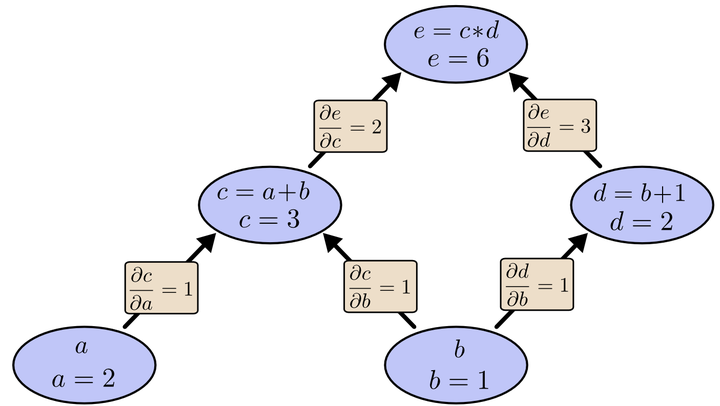
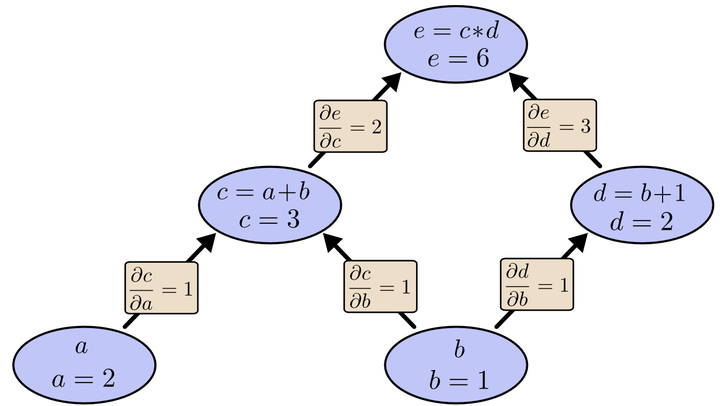
   具体理解：如果individual one和individual two有关联，生成variable node：action variable(y)=a、b, interactive variable(z)=g(a, b); factor node：F_y=(a, b, g(a, b)), F_z=((a, b)，(a, c)，(b, c))，那么edge就应该是图1中green solid lines

​ 图1 TOGN(三个individual)

1.2 图的构建

图的构建主要两部分，一部分是initialized base feature(被送进第一层TOGN的，利用图特性来传递更新)，另一部分是图的structure，即索引构建(如何对无序的initialized base feature建立关联性)

这部分主要解释索引构建

首先建立索引n+2×Cn2+Cn3个条目（代码里是从0开始索引）

索引条目可分为四个part，对应四个node类型：V_y、V_z、F_y、F_z

1
2
3
4

n[0,n-1],(variable node-y) number=n
z[n,n+n*(n-1)/2-1],(variable node-z)  number=Cn2
h[n+n*(n-1)/2,n+n*(n-1)-1],(factor node-y) number=Cn2
g[n+n*(n-1),n+n*(n-1)+(n*(n-1)*(n-2)/6)-1], (factor node-z) number=Cn3

For example：

1.从variable node-y到variable node-z

假设有5个individual，即n=5个(variable node-y)，V_y={0,1,2,3,4}

1

h_id={ c:i+N for i,c in enumerate(combinations(range(N),2))}

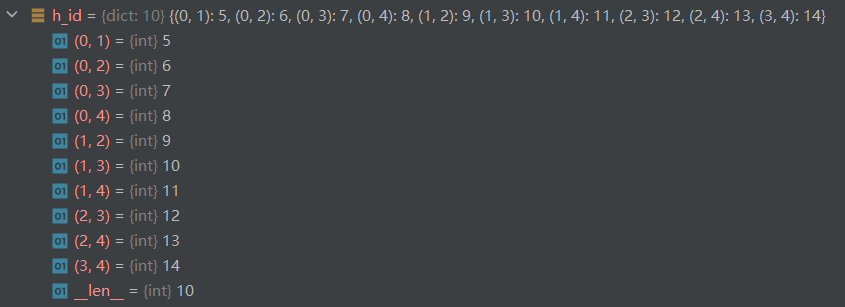
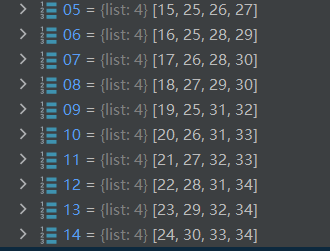
如下图，n个individual进行二元组合，得到10个variable node-z；

以dictionary的key-value形式存储，key=(i, j)，value=索引(在整个索引条目中的位置)；

ps1：因为V_y={0,1,2,3,4}占据了索引条目中index: 0-4,，V_z排在V_y后面，就从index=5开始

ps2：这张图仅为Graph构建前提，不是Graph本身

2.构建Graph

Graph-G索引本质上是一定数量的list(共n+2×Cn2+Cn3，有多少node，就有多少list)，对应了所有类型的node，即V_y、V_z、F_y、F_z四个part。

1

G=[[] for _ in range(N+N*(N-1)+N*(N-1)*(N-2)//6)]

问题：这些list的内容是什么，即每个node存放什么

举例子：

factor node-y=(i, j, g(i, j))，在Graph索引中factor node-y的起始位置为hidx=n+Cn2（前面是V_y、V_z的位置），那么G[hidx]=????，即i=? j=? g(i, j)=?；G[hidx]=[u,v,h_id[(u,v)]]

若n=5(总共有5个人)，在G中，第一个factor node-y的位置hidx=15，G[15]=[0,1,5]；

因为根据从variable node-y到variable node-z部分的解析，5个人两两组合，得到key=(0,1)(0,2)..(individual one索引，individual two索引)…(3,4)，value=5、6..individual combination在G中存放位置..13、14，总共10个key-value存储数据((两层for循环是按顺序组合5个人，第一个人的索引=0，第二个人索引=1))

那么F_y存储的就是(individual one索引(u)，individual two索引(v)，combination在G中存放位置(h_id[(u,v)]) )

————————————————————————————————————————–>

那么variable node-y和variable node-z存放什么？

1.variable node-y存放factor node-y的索引；

假如individual one索引(u)，individual two索引(v)构成了一个factor node-y，该F_y的位置是G中第hidx个list—->G[hidx]，那么G[u]=hidx,G[v]=hidx

ps1：一个人可以构成很多个F_y，例如第一个人(index=0)，可以构成factor node=(0,1,5)/(0,2,5)，则G[u]存储的hidx是所有与点u有关的F_y的索引

ps2：第u个individual实际会参与N-1个variable node-z构成，即G[u]:N-1个factor node-y的编号

V_y: ‘all’ related labels of F_y

2.variable node-z存放factor node-y的索引；

同理，跟V_y存放内容一样，V_z存放与自己有关的F_y的索引

1
2
3
4
5
6
7
8
9
10

hidx=N+N*(N-1)//2 #factor node-y的起始label n+Cn2
for u in range(N):  #V_y,individual one
    for v in range(u+1,N): #V_y,individual two
        # k=g(u,v),u,v∈V_y,k表示two individual interaction,=(0/1)
        # 在G的第hidx个[]中，extend[u,v,h_id[key]],key->(u,v)则hi_d[key]表示第u、v个			individual构成了variable node-z中的第h_id[(u,v)]个z-node
        G[hidx].extend([u,v,h_id[(u,v)]]) #F_y,factor node-y
        G[u].append(hidx) #第u个individual,对应第hidx(编号)个factor node-y,即[u,v,g(u,v)]
        G[v].append(hidx) #第v个individual,对应第hidx(编号)个factor node-y
        G[h_id[(u,v)]].append(hidx) #第h_id[(u,v)个V_z,对应第hidx(编号)个factor node-y
        hidx+=1 #下一个factor node-y

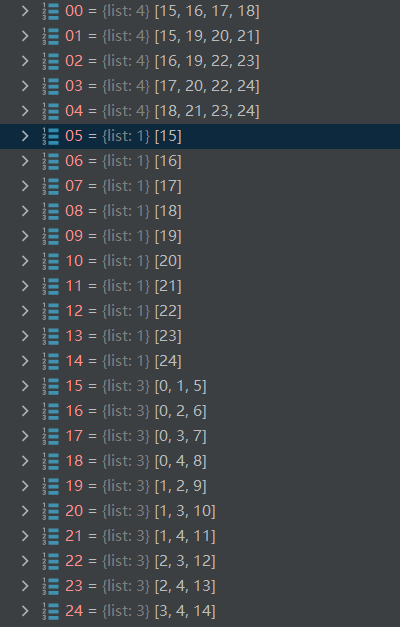
如下图，

0-4代表V_y：存放related index of F_y

5-14代表V_z：存放related index of F_y

15-24代表F_y：存放index of V_yu V_yv and F_y

————————————————————————————————————————–>

剩下factor node-z存放什么还不知道？？？？

factor node-z=((i,j), (i,k) ,(j,k)) 的索引从gidx=n+2×Cn2开始，G[gidx]=[z1,z2,z3]

ps：(i,j)指的是两个individual组成的V_z的索引

假如n=5，gidx=25，G[25]=[5,6,9];

因为individual one索引=0，individual two索引=1，individual three索引=2，组合得到(0,1)(0,2)(1,2)，根据1.从variable node-y到variable node-z图中可以得知，h_id[(0,1)]、h_id[(0,2)]、h_id[(1,2)]分别对应5、6、9(三个V_y组合成的三个V_z在G中的索引位置)

为了保持关联性，G中V_z的位置要添加F_z的索引gidx：G[z1].append(gidx)、G[z2].append(gidx)、G[z3].append(gidx)

1
2
3
4
5
6
7
8
9
10

gidx=N+N*(N-1) #factor node-z的起始label n+2*Cn2
for i in range(N): #V_y,individual one
    for j in range(i+1,N): #V_y,individual two
        for k in range(j+1,N): #V_y,individual three
            z1,z2,z3=h_id[(i,j)],h_id[(i,k)],h_id[(j,k)] #三组 individual_pair 的variable node-z的label
            G[gidx].extend([z1,z2,z3]) #F_z,factor node-z
            G[z1].append(gidx) #第z1个variable node-z,对应第gidx(编号)个factor node-z,即[g(i,j),g(i,k),g(j,k)]
            G[z2].append(gidx) #第z2个variable node-z,对应第gidx(编号)个factor node-z
            G[z3].append(gidx) #第z3个variable node-z,对应第gidx(编号)个factor node-z
            gidx+=1 #下一个factor node-z

V_z: related labels of F_y(only one) + ‘all’ related labels of F_z

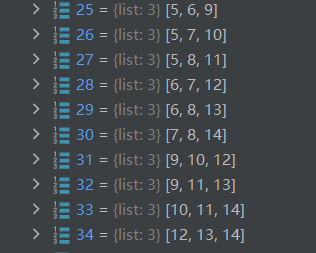
25-34代表F_z：存放n(=5)个individual进行Cn3组合后，再Cn2组合得到的三个二元组(a,b)(a,c)(b,c)在G中的索引

​ 图 Graph中的factor node-z

5-14代表V_z：在存放了index of related F_y之后，存放index of related F_z，比如index=5代表的(0,1)组合，总共5个人，除去0, 1还剩3个，(0,1)作为整体和剩下三个组合，得到3个三元组，即三个F_z，那么index=5的V_z就需要关联3个F_z的index=25,26,27

​ 图 Graph中的关联factor node-z后的variable node-z

创建子文件夹new文章：hexo new post -p ./LeetCode学习/Tree前中后序遍历.md

前序遍历

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

class Solution {
public:
    vector<int> preorderTraversal(TreeNode* root) {
        vector<int> res;
        if(root == nullptr) return res;

        stack<TreeNode*> stk;
        TreeNode* node = root;

        while(!stk.empty() || node != nullptr){
            while(node != nullptr){
                res.push_back(node->val);
                stk.push(node);
                node = node->left;
            }
            node = stk.top();
            stk.pop();
            node = node->right;
            
        }
        return res;
    }
};

中序遍历

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

class Solution {
public:
    vector<int> inorderTraversal(TreeNode* root) {
        vector<int> res;
        stack<TreeNode*> sta;

        while(root!=nullptr || !sta.empty()){
            while(root != nullptr){
                sta.push(root);
                root = root->left;
            }

            root = sta.top();
            sta.pop();
            res.push_back(root->val);
            root = root->right;
        }

        return res;
    }
};

后序遍历

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

class Solution {
public:
    vector<int> postorderTraversal(TreeNode* root) {
        vector<int> res;
        stack<TreeNode*> stk;
        TreeNode* node = root;
        TreeNode* pre = nullptr;

        while(!stk.empty()|| node!=nullptr){
            while(node !=nullptr){
                stk.push(node);
                node= node->left;
            }
            node = stk.top();
            stk.pop();
            if(node->right==nullptr || pre == node->right){
                res.push_back(node->val);
                pre=node;
                node=nullptr;
            }
            else{
                stk.push(node);
                node = node->right;
            }
        }
        return res;
    }
};

5.操作符重载和临时对象

传递者，无需知道接受者是以reference形式来接收

function的返回值：需不需要返回（void or xxx）->

​ 返回by value or by reference->

​ 返回结果const or not

07.三大函数：拷贝构造，拷贝赋值，析构

1.dataset准备

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38

source scripts/prepare_data.sh

----------------->
mkdir -p data  //在VIBE文件夹下创建data文件夹
cd data
gdown "https://drive.google.com/uc?id=1untXhYOLQtpNEy4GTY_0fL_H-k6cTf_r"//这个我直接电脑下载，传到服务器的
unzip vibe_data.zip //解压出一个vibe_data文件夹
rm vibe_data.zip
cd ..
mv data/vibe_data/sample_video.mp4 .//无用代码
mkdir -p $HOME/.torch/models/ 
mv data/vibe_data/yolov3.weights $HOME/.torch/models/


source scripts/prepare_training_data.sh //这部分data处理需要vibe_data文件夹的东西

------------------------------------>
mkdir -p ./data/vibe_db
export PYTHONPATH="./:$PYTHONPATH"

# AMASS（discriminator DATASETS）//数据集目标不一致
python lib/data_utils/amass_utils.py --dir ./data/amass

# InstaVariety（DATASETS_2D）//直接下载18G的处理后的数据，到vibe_db
# Comment this if you already downloaded the preprocessed file
python lib/data_utils/insta_utils.py --dir ./data/insta_variety

# 3DPW（DATASET_EVAL）//下载imagefiles和sequencefiles，然后跑这行代码就行
python lib/data_utils/threedpw_utils.py --dir ./data/3dpw

# MPI-INF-3D-HP（DATASETS_3D）//下载压缩包里有.sh脚本文件，需要利用脚本下载，还要先把里面的config的0变成1，才能下载；下载完还需要一个sh提取extract_mpi_inf_3dhp_frames.py，然后再用pre.sh处理
python lib/data_utils/mpii3d_utils.py --dir ./data/mpi_inf_3dhp
----------------------------------->以下没啥用
# PoseTrack
python lib/data_utils/posetrack_utils.py --dir ./data/posetrack

# PennAction
python lib/data_utils/penn_action_utils.py --dir ./data/penn_action

卷积层（convolution layer）

填充（padding）

作用：因为深度学习的模型里会有很多层cov layer，而每层cov layer都会让原来的图变小（比如，33×33的picture，用 5×5的kernel，会产生28×28(33-(5-1))的新picture）。为了不让picture在许多层cov layer后变得太小，就会在输入周围额外添加行/列

为了使输出的picture size 和输入相同，padding 的大小通常取kernel size-1(kh-1,kw-1)

步幅（stride）

一般为2的倍数，成倍的减少输出size

多通道

多输入

RGB图像就有三个通道，每个通道对应一个kernel（注意：RGB是三通道，可以看成一个feature map，H×W×D，深度不为1，filter可以看做是包含深度的kernel，而filter深度=feature map深度，即a×b×D，），结果是所有通道卷积结果的和

多输出

前提:多输出和多输入没直接关联性

多输出举例：RGB三通道（三个2维kernel==一个3维kernel）经过3维kernel，得到3个结果，然后求和（得到一个2维结果），如果对RGB图像，使用n个3维kernel，得到n个2维结果(一个2维结果就是一个3维kernel（一个filter）计算得到的)

多输入和多输入结合理解

多输出通道：不同的kernel识别重点不同，比如有的输出猫头特征，有的输出猫尾巴特征

多输入通道：将输出通道的多个输出，进行权重相加，得到组合的特征

池化

缓解卷积层对位置的敏感性（一般放在cov layer后面）

二维最大池化（当然还有平均池化层）

池化层也可以包括padding、stride；如果有多输入通道，每个input channel经过池化层后，直接得到输出（输出数量=输入通道数，不同于cov layer->将多输入卷积结果合成一个结果），因此，有输入->池化->输出(输入通道数=输出通道数)

1×1卷积

升维/降维

用一个<1×1×同feature map深度>的filter，对feature map卷积，可以将feature map深度变成1（注意：因为feature map深度为3，像RGB图一样，深度为3的filter（或者说3个1×1的kernel）卷积，是将对3个深度为1的56×56图卷积后，将结果线性相加的到深度为1的输出的）；

用二个filter，可以得到56×56×2的结果(因为结果的深度都小于3，所以是降维)

用n个>3的filter，可以得到56×56×n的结果，是升维

学习资源：

1. （全面）Machine Learning：，Tom M. Mitchell 机械工业出版社 2003年
2. 统计学习方法，李航，清华大学出版社，2012
3. Machine Learning：A Probabilistic Perspective，K.P Murphy
4. 视频课程：Stanford web course by Andrew Ng
5. 视频课程：Stanford web course by Fei-fei Li

没有免费午餐定理（No Free Lunch Theorem）

如果我们不对特征空间有先验假设，则所有算法的平均表现是一样的

支持向量机（Support Vector Machine）

在样本数比较少的情况下，可以得到比较好的结果（小样本方法）

支持向量机

1.线性模型

线性可分：训练集和样本集可以用一条直线分开

2.非线性模型

线性不可分：训练集和样本集不可以用一条直线分开

理论关键点1：如何定义一条线，将训练集和样本集恰当的分开（恰当=在误差上，不偏袒训练或者样本集任一方）

答：

定义一个衡量指标——向训练集和样本集的方向，分别平移此线，在刚好碰到训练集和样本集的某些点时，能够使平移后的两条线距离最大

符合衡量指标的线条有很多（平行线），如何确定一条恰当的线——取所有平行线中，最中间的那条（到训练集和样本集距离相等的那条）

间隔d定义：关键点1中的分割线，向到训练集和样本集平移，刚好分别与训练集和样本集的某些点相碰，产生的两条平行线间的距离

支持向量定义：分割线的所有平行线之中，刚好分别与训练集和样本集的某些点相碰的两条平行线碰到的点，所代表的向量（support vectors）

ps：正是因为分割线的定义只是基于支持向量（支持向量仅占训练集和样本集的少部分），所以支持向量机依靠少量数据就能实现

内容概述

神经网路与多层感知机：基础知识、激活函数、反向传播、损失函数、权值初始化和正则化
卷积神经网络、循环神经网络
人工智能>机器学习>人工神经网络（以神经元形式连接的机器学习模型）>深度学习

学习资源：

1. 吴恩达 www.deeplearning.ai
2. 李宏毅 B站搜索
3. 花书《deep learning》https://github.com/exacity/deeplearningbook-chinese
4. 西瓜书《机器学习》周志华

人工神经网络

概念：

perception（感知机）

activation function（激活函数）

back propagation（反向传播）

激活函数

激活函数引用目的：

1. 令多层感知机真正的成为多层，而不是退化为一层
2. 引入非线性，使网络可以逼近任意非线性函数（万能逼近定理，universal approximator）

激活函数需要具备的性质：

1. 连续并可导（允许少数点不可导），便于利用数值优化的方法学习网络参数（什么叫数值优化？）
2. 激活函数和其导函数要尽量简单，有利于提高网络计算效率
3. 激活函数的导函数的值域要在合适区间，否则会影响训练效率和稳定性

常见激活函数：

Sigmoid函数、tanh函数、Relu函数

单层感知机

输入*权重=输出（无隐藏层）

F（<Xn·Wn>+偏置b）=O——以向量乘法<A·B>（单行矩阵乘法）来表示单层感知机计算，再放进F函数（激活函数）

上图为单层感知机，其缺点：无法解决异或问题

多层感知机（Multi Perception，MLP）

在单层感知机的基础上，添加一个或多个隐藏层

输入 * 权重 = 输出（隐藏层1）—>隐藏层1 * 权重 = 输出（隐藏层2）…隐藏层n * 权重=输出层

矩阵表示：X1*n表示输入矩阵；W1n*m表示权重矩阵(n-输入，m-输出)；H1*m表示隐藏层矩阵；W2m*k；O1*k表示输出矩阵

​ X*W1+b1=H

​ H*W2+b2=O(b是偏置项)

ps：这部分其实不对，输入*权重的结果经过activation function 才会成为H

多层感知机的激活函数：如果无激活函数，多层感知机会退化为单层网络，
$$
\begin{aligned}
\mathbf{H} &=\mathbf{W}{1} \mathbf{X}+\mathbf{b}{1}\
\mathbf{O} &=\mathbf{W}{2} \mathbf{H}+b{2} =\mathbf{W}{2}(\mathbf{W}{1} \mathbf{X}+\mathbf{b}{1})+\mathbf{b}{2} =\mathbf{W}{2}\mathbf{W}{1}\mathbf{X}
+\mathbf{W}{2}\mathbf{b}{1}+\mathbf{b}_{2}
\end{aligned}
$$
X经过两层权重计算输出结果O，通过计算，结果可以等效成X经过W1W2的乘积（即一层权重网络），然后加上后半部分，也就是说，X经过两层网络，但实际结果可以等效成经过一层网络，这就叫退化成单层网络

所以在经过第一层权重计算后，要通过激活函数（为什么W2要转置呢？）
$$
\begin{aligned}
\mathbf{H} &=\mathbf{F}\left(\mathbf{W}{1} \mathbf{X}+\mathbf{b}{1}\right) \
\mathbf{O} &=\mathbf{W}{2}^{T} \mathbf{H}+b{2}
\end{aligned}
$$

反向传播（Back propagation）

机器学习可以看做是数理统计的一个应用。在数理统计中一个常见的任务就是拟合，也就是给定一些样本点，用合适的曲线（函数）揭示这些样本点随着自变量的变化关系。

深度学习同样也是为了这个目的，只不过此时，样本点不再限定为(x, y)点对，而可以是由向量、矩阵等等组成的广义点对(X,Y)。而此时，(X,Y)之间的关系也变得十分复杂，不太可能用一个简单函数表示。然而，人们发现可以用多层神经网络来表示这样的关系，而多层神经网络的本质就是一个多层复合的函数。借用网上找到的一幅图，来直观描绘一下这种复合关系。

表达式如下（输入x经过加权相乘，然后加偏置向，然后通过激活函数）：

式中的Wij就是相邻两层神经元之间的权值，它们就是深度学习需要学习的参数，也就相当于直线拟合y=k*x+b中的待求参数k和b。

和直线拟合一样，深度学习的训练也有一个目标函数，这个目标函数定义了什么样的权值参数才算一组“好参数”，在机器学习中，一般是采用损失函数（cost function）作为目标，然后，训练目标就是通过调整每一个权值Wij来使得cost达到最小。cost函数也可以看成是由所有待求权值Wij为自变量的复合函数，而且基本上是非凸的，即含有许多局部最小值。但实际中发现，采用我们常用的梯度下降法？就可以有效的求解最小化cost函数的问题。

梯度下降法需要给定一个初始点，并求出该点的梯度向量，然后以负梯度方向为搜索方向，以一定的步长进行搜索，从而确定下一个迭代点，再计算该新的梯度方向，如此重复直到cost收敛。那么如何计算梯度呢？

假设我们把cost函数表示为, 那么它的梯度向量就等于, 其中表示正交单位向量。为此，我们需求出cost函数H对每一个权值Wij的偏导数。而BP算法正是用来求解这种多层复合函数的所有变量的偏导数的利器。

求cost最小值——>使用梯度下降法——>求初始点梯度——>求cost函数对权值W的偏导数——>使用BP算法

概念：从损失函数开始，从后向前传输梯度到第一层

作用：更新权重，使网络输出更接近标签（label）

反向传播的基本原理：微积分的链式求导法则
$$
\begin{equation}
y=f(u), u=g(x) \quad \frac{\partial y}{\partial x}=\frac{\partial y}{\partial u} \frac{\partial u}{\partial x}
\end{equation}
$$
举例子：

作者：Anonymous
链接：https://www.zhihu.com/question/27239198/answer/89853077
来源：知乎

我们以求e=(a+b)*(b+1)的偏导为例。
它的复合关系画出图可以表示如下：

在图中，引入了中间变量c,d。

为了求出a=2, b=1时，e的梯度，我们可以先利用偏导数的定义求出不同层之间相邻节点的偏导关系，如下图所示。

利用链式法则我们知道：
以及。

链式法则在上图中的意义是什么呢？其实不难发现，的值等于从a到e的路径上的偏导值的乘积，而的值等于从b到e的路径1(b-c-e)上的偏导值的乘积加上路径2(b-d-e)上的偏导值的乘积。也就是说，对于上层节点p和下层节点q，要求得，需要找到从q节点到p节点的所有路径，并且对每条路径，求得该路径上的所有偏导数之乘积，然后将所有路径的 “乘积” 累加起来才能得到的值。

这样做是十分冗余的，因为很多路径被重复访问了。比如上图中，a-c-e和b-c-e就都走了路径c-e。对于权值动则数万的深度模型中的神经网络，这样的冗余所导致的计算量是相当大的。

同样是利用链式法则，BP算法则机智地避开了这种冗余，它对于每一个路径只访问一次就能求顶点对所有下层节点的偏导值。
正如反向传播(BP)算法的名字说的那样，BP算法是反向(自上往下)来寻找路径的。

从最上层的节点e开始，初始值为1，以层为单位进行处理。对于e的下一层的所有子节点，将1乘以e到某个节点路径上的偏导值，并将结果“堆放”在该子节点中。等e所在的层按照这样传播完毕后，第二层的每一个节点都“堆放”些值，然后我们针对每个节点，把它里面所有“堆放”的值求和，就得到了顶点e对该节点的偏导。然后将这些第二层的节点各自作为起始顶点，初始值设为顶点e对它们的偏导值，以”层”为单位重复上述传播过程，即可求出顶点e对每一层节点的偏导数。

以上图为例，节点c接受e发送的12并堆放起来，节点d接受e发送的13并堆放起来，至此第二层完毕，求出各节点总堆放量并继续向下一层发送。节点c向a发送21并对堆放起来，节点c向b发送21并堆放起来，节点d向b发送31并堆放起来，至此第三层完毕，节点a堆放起来的量为2，节点b堆放起来的量为21+3*1=5, 即顶点e对b的偏导数为5.

举个不太恰当的例子，如果把上图中的箭头表示欠钱的关系，即c→e表示e欠c的钱。以a, b为例，直接计算e对它们俩的偏导相当于a, b各自去讨薪。a向c讨薪，c说e欠我钱，你向他要。于是a又跨过c去找e。b先向c讨薪，同样又转向e，b又向d讨薪，再次转向e。可以看到，追款之路，充满艰辛，而且还有重复，即a, b 都从c转向e。

而BP算法就是主动还款。e把所欠之钱还给c，d。c，d收到钱，乐呵地把钱转发给了a，b，皆大欢喜。

学习率

作用：控制更新步长（通常小于1）

xi+1=xi-k*f’(xi)

损失函数（Loss function）

损失函数：衡量模型与真实标签之间的差异（针对单样本）
$$
\begin{aligned}
\mathbf{Loss} &=\mathbf{f}\left(\mathbf{y}{o},\mathbf{y}\right) \
\end{aligned}
$$
代价函数（cost function）：针对样本总体
$$
\begin{aligned}
\operatorname{Cost} =\frac{1}{N} \sum{i}^{N} f\left(y_{o}, y_{i}\right)
\end{aligned}
$$
目标函数（objective function）Obj=Cost（要小）+Rgularization Term(正则项，让模型不会过于复杂)

常见损失函数

1. MSE（mean square error）均方误差

$$
M S E=\frac{\sum_{i=1}^{n}\left(y_{o}-y_{lable}\right)^{2}}{n}
$$

2. CE（cross entropy ）交叉熵

$$
H(p, q)=-\sum_{i=1}^{n} p\left(x_{i}\right) \log q\left(x_{i}\right)
$$

为什么用交叉熵来衡量两种分布之间的差异（p表示目标分布，q表示计算出来的分布——要让q逼近p）
$$
\begin{aligned}
&D_{K L}(P | Q)=E_{x-p}\left[\log \frac{P(x)}{Q(x)}\right]=E_{x \sim p}[\log P(x)-\log Q(x)] \
&=\sum_{i=1}^{N} \mathrm{P}\left(\mathrm{x}{i}\right)\left(\log P\left(\mathrm{x}{i}\right)-\log \mathrm{Q}\left(\mathrm{x}{i}\right)\right) \
&H(p, q)=-\sum{i=1}^{n} p\left(x_{i}\right) \log q\left(x_{i}\right) \
&H(\mathrm{x})=E_{x-p}[I(x)]=-E[\log P(x)]=-\sum_{i=1}^{N} p_{i} \log \left(p_{i}\right)
\end{aligned}
$$
相对熵DKL+信息熵H(x) = 交叉熵H(p,q)

优化交叉熵等价于优化相对熵（因为H(P)作为要逼近的目标，信息是确定的）

模型输出的结果可能大于1，不符合概率分布的形式，即无法用交叉熵的形式计算

所以Softmax函数可以实现将数据变换到符合概率分布的形式
$$
y_{i}=S(\boldsymbol{z}){i}=\frac{e^{z{i}}}{\sum_{j=1}^{C} e_{j}^{z_{j}}}, i=1, \ldots, C
$$

权值初始化

随机初始化：从高斯分布中随机采样，对权重赋值，随机初始化（3σ准则：数值分布在均值μ左右3σ的概率要达到99.73%）——初始权重不能太大，不然后面计算结果经过激活函数后，会达到饱和区，梯度就近乎没有了

随机分布的标准差会影响权重大小，如何设置标准差

自适应标准差：Xavier初始化、Kaiming初始化（MSRA法）

正则化方法（Regularization）

正则化是为了减小方差，即减轻过拟合（方差过大导致训练集表现好，测试集表现不好）的方法

误差=偏差+方差+噪声

偏差：度量了学习算法的期望预测与真实结果的偏离程度，即刻画了学习算法本身的拟合能力

方差：度量了同样大小的训练集的变动所导致的学习性能的变化，即刻画了数据扰动所造成的影响

噪声：则表达了在当前任务上任何学习算法所能达到的期望泛化误差的下界

方法1.在目标函数后添加regularization term：

regularization term分L1、L2两种

L1:|Wi|求和

L2:|Wi^2^|求和，也成为权值衰减（weight decay）

方法2.随机失活（dropout）

作用：避免模型过度依赖某个神经元，减轻过拟合

随机的令神经元失活（即将神经元前的权值设为0）

ps：训练和测试时数据尺度会变化（测试时不会执行权重失活操作），所以测试时，神经元输出值要乘P才好对比测试和训练两数据结果？（p为随机失活的概率）

其他正则化方法：batch normalization、layer normalization、instance normalization group normlizaiton

拼音打字

介绍

一个字的读音称：音节（朱——zh+u，第一声）

所有字的音节分三种：1.双音节（声母+韵母） 3.单音节（没声母，只有韵母） 4.三音节（声母+介母+韵母）

a 啊 单音节
m+a 妈 双音节
l+i+ang 亮 三音节

声母：文字拼音的开头读音

韵母：文字拼音的末尾读音

范例：房（f+ang，第二声）——>“f”是声母，“ang”是韵母

音调

妈 mā 【第一声】 麻 má 【第二声】 马 mǎ 【第三声】 骂 mà 【第四声】 吗 ma 【轻读声】

在按键打字时，是不分音调的。例如：输入m+a，手机会显示 ‘ma’ 这个发音的所有音调字（包括妈、麻、马、骂、吗）

两、三拼音节的结构

主要以声母+(介母，两拼音节不用这个)+韵母

声母表

在汉语拼音中，英文字母用中文发音，例如：b应当读成波

介母表(在三拼音节中使用)

韵母表（打字专用）

整体认读音节表

yun[晕]　ye[叶]　yue[月]

自成音节

只有以ɑ、o、e开头的韵母，可以加声母，独立自成一个音节,如阿ā、爱ài、袄ǎo、安ān、哦ò、欧ōu、鹅é

三拼音节

手机按键

九键

从第一行第二列往右，到顶，再从第二行开头往右，再从第三行往右

这是26个英文字母的正常顺序

二十六键盘

对于在Hexo博客内插入图片，我在网上看了一些别人的方法，总结下我如何利用Typora实现在Hexo中插入图片的

Hexo博客搭建完毕之后，需要选择一款支持Markdown语法的工具来编辑博客文章（总不能在命令窗口里面写吧）。我选择的是Typora。

首先在\source_posts里创建一篇文章，Git Bash输入命令

1

hexo -n “如何在hexo博客内插入图片”

生成

注意：图片的路径应该为../images开头(所有路径必须用///这种斜杠，\\不行)，因为github仓库里，如果想要引用图片，则需要../前往上一级目录，然后在此目录下寻找images目录，然后在images里面寻找同名目录，然后引用图片

然后用Typora打开这个.md后缀的文件

1. Typora设置

   打开右上角文件选择偏好设置(preference)，选择图像，选择复制到指定路径，输入../../source/images/${filename}，然后右上角X掉就行。

   解释下操作的含义：Typora是可以通过很多方式将图片插入到文本里的，当将图片拖动进来是的时候，会自动在source/images目录下生成一个与文章同名的文件夹，并将插入的图片复制一份到该文件夹里（我不知道为什么我把图拖进typora，图片会一直显示copying），${filename}表示文章名字

2. Hexo设置-安装插件

   1	npm install hexo-renderer-marked --save

   然后打开_config.yml文件（之前为了推送博客到github，在里面设置过git和repo）

   把下面的复制进去（可能postAsset不用加，加上试试吧）

   1 2 3

   marked: prependRoot: true postAsset: true

   

下面是两个参数的含义（postAsset可能真的不用加）

• prependRoot

  - Prepend root value to (internal) image path.

  • Example _config.yml:

  1	root: /blog/

  • ![text](/path/to/image.jpg) becomes <img src="/blog/path/to/image.jpg" alt="text">

• postAsset

  - Resolve post asset’s image path to relative path and prepend root value when

  post_asset_folder

  is enabled.

  • “image.jpg” is located at “/2020/01/02/foo/image.jpg”, which is a post asset of “/2020/01/02/foo/“.
  • ![](image.jpg) becomes <img src="/2020/01/02/foo/image.jpg">
  • Requires prependRoot to be enabled.

3. 最后一步

   因为我的typora不知道为什么，拖动进来图片后，虽然，source/images目录下自动创建了同名文件夹，但是图片死活copy不进去（一直显示copying）。

   所以我就自己把图片到source/images//${filename}下面了，然后从里面把图片拖进typora编辑的文章里

   到这里图片是拖进来，但是typora不显示（实际直接hexo g -d推送github，是可以在博客内显示的），因为typora有地方没设置

​ 解决方法：点开typora上面的格式，然后选图像，点击设置图片根目录，选择source目录，然后图片就 能在typora内显示了

到这里，基本typora和hexo两个部分的设置就完成了，然后hexo g -d生成推送

github博客效果如下

首先感谢codesheep（B站up）的视频指导

本流程是windows下完成的，在实现过程中碰到了一些问题，使用了别人的解决方法，所以这篇博客是个自我学习总结

一开始是用cmd窗口输入命令的，然后发现用Git Bash更好（之前学过linux的命令语言），所以建议安装Git Bash之后，在Git里面操作（安装完成后，先完成6.4的配置再从头看）

1.首先下载Node.js

网址：Node 下载LTS版本

直接全部点next（自己修改下安装路径），然后完成安装

检查安装结果：打开Git Bash 输入命令

1
2

node -v ##检查node安装的版本
npm -v  ##检查npm（node package manager）安装的版本

npm(node安装完自带的)是用来安装之后所需包的工具(基于Node.js的javascript代码包管理工具)

如果下载是.msi格式的安装包，，那么Node会自动在系统变量path中添加安装路径（如果变量添加成功，则上面查node版本肯定可以成功）

2.Node环境配置

配置目标：npm安装的全局模块的路径、缓存cache的路径（将npm安装的东西，放到Node的安装路径，统一管理）

环境配置的理由：在执行类似：npm install -g XXXX （后面的参数-g，代表global全局安装的意思）的安装语句时，会将安装的模块安装到【C:\Users\用户名\AppData\Roaming\npm】路径中（因为用户变量Path内，node默认配置了C:\Users\用户名\AppData\Roaming\npm作为模块的安装路径）。主要是不想在用npm装东西时，把东西自动放C盘占地方

1. 创建两个文件夹【Node.js安装路径】下创建两个文件夹【node_global】及【node_cache】

创建两个文件夹之后，Git Bash 输入命令

1
2

npm config set prefix "node安装路径\node_global"
npm config set cache "node安装路径\node_cache"

以上操作表示：修改全局包下载目录为安装路径\node_global,缓存目录为安装路径\node_cache,输入上面命令后会自动创建node_global目录，而node_cache目录会在下载全局包时自动创建

2. 修改环境变量

   在环境变量—>系统变量下新建NODE_PATH，值：Node安装路径\node_global\node_modules

   在环境变量—>用户变量下的Path内，将C:\Users\用户名\AppData\Roaming\npm修改为Node安装路径\node_global

3. 测试修改效果

   在Git Bash内输入

   1	npm install -g express

   

   在node安装路径\node_global\node_modules内出现了express的包，说明环境配置成功，以后新装的package都会出现在这个目录下

3.更换npm源

1-2中完成了Node的下载和环境配置，接下来就要用Node的工具npm来安装hexo博客框架了。但是，因为用npm下载慢，所以装阿里的镜像npm->cnpm，

注意事项，在利用npm装东西的时候，应该将Git Bash通过管理员模式打开

Git Bash输入命令如下

1

npm install -g cnpm --registry=https://registry.npm.taobao.org

cnpm包就会出现在与express相同的地方（同样可以通过cnpm -v的形式查验安装版本）

4.安装Hexo

安装好cnpm后，就可以用cnpm的命令下载hexo了

Git Bash输入命令

1

cnpm install -g hexo-cli

安装完可以通过hexo -v验证，hexo包会出现在与express相同的地方

5.创建本地博客

下载好hexo之后，找个地方创建一个文件夹-我命名为Blog，Git Bash通过cd命令进入Blog路径下（一定要进入Blog文件夹的路径下）

输入下面命令，会在Blog文件夹下，初始化hexo博客架构（会自动生成一个hello world的博客）

1

hexo init

如果要创建自己的博客，首先通过cd命令进入路径Blog/source/_posts（文章都放在这个目录下）

输入命令

1

hexo n "我的第一篇博客"

然后输入下面命令，生成刚创建（new）的博文

1
2
3

hexo clean ##清理缓存 
hexo g ##创建generate
hexo s ##启动server

然后在浏览器中打开链接http://localhost:4000/，就可以看到自己的博客了

6.创建Github博客

1. 在注册github账户后，创建仓库create a new repository

   用户部署个人博客的gihub仓库的命名必须符合特定要求，即repository name：owner name.github.io

   例如：owner：qingjiu 那么 repository name必须为qingjiu.github.io

2. 安装github的插件

   在Blog目录下安装，输入如下命令

   1	cnpm install --save hexo-deployer-git

   这个可以帮助把本地博客推送（deploy）到github

3. 配置_config.yml文件

   1	vim _config.vml ##进入_config.yml文件

   找到deploy的下面

   在type：后写git

   添加repo：写自己github仓库的HTTPS地址，例如https://github.com/flybigpig1999/flybigpig1999.github.io.git

   添加brach：maser（冒号后面要空一格）

   1 2 3 4 5

   deploy: type: git repo: <repository url> #https://bitbucket.org/JohnSmith/johnsmith.bitbucket.io branch: [branch] message: [message]

4. 配置Git（全篇都是用Git Bash来输入命令，所以应该在最开始安装Git就配置好）

   在安装完Git后应当首先配置下Git的个人信息，在Git Bash内输入如下命令

   1 2	git config --global user.name ##在user.name处写自己的github名字 git config --golbal user.email ##在user.email处写自己的github注册邮箱

   如果想要查询Git的config信息，输入

   1	git config --list

5. 将本地博客推送到github

   在推送本地博客到github之前，想要免密推送，需要生成秘钥

   Git Bash输入秘钥生成

   1	ssh-keygen -t -ras -C "你的github注册邮箱"

   然后一直回车，系统会自动在C:\Users\用户\目录下生成**.ssh文件夹 **

   地址：C:\Users\jhon.ssh

   用记事本打开id_rsa.pub（公共秘钥），复制给出的所有文本，登录github，在右上角用户图标下拉栏目里找到Settings

   

   然后在左侧栏目，找到SSH and GPG keys，创建SSH keys（title随便取，Key栏里粘贴刚才复制的公共秘钥）

   

   粘贴好之后确认生成秘钥，然后可以通过在Git Bash输入命令

   1	ssh -T git@github.com

   检测连接是否成功

   如果出现下面这种情况（connection refused连接被拒绝）

   

   可以输入下面的命令

   1	ssh -vT git@github.com

   修复完之后再输入-T的命令，重新验证是否连接成功

   

   这样就是成功了successfully，然后就可以免密推送（deploy）博客到github了

   1	hexo d ##在hexo g之后推送；hexo s仅仅是本地查看，会一直运行，需要Ctrl+C退出

   最后，可以在链接为：用户名.github.io 下查看github博客的内容

   至此，基于github的hexo博客就搭建完成了！